FCSys.Species
Dynamic models of chemical speciesInformation
Extends from Modelica.Icons.Package (Icon for standard packages).Package Content
| Name | Description |
|---|---|
| C | |
| C19HF37O5S- (abbreviated as SO3-) | |
| e- | |
| H+ | |
| H2 | |
| H2O | |
| N2 | |
| O2 | |
| Base model for an ion | |
| Base model for a fluid species | |
| Base model for an inert, stationary solid | |
| Base model for one chemical species in one phase | |
| Choices of options |
 FCSys.Species.Ion
FCSys.Species.Ion
Base model for an ion

Information
Please see the Fluid model.
Extends from Fluid (Base model for a fluid species).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Integer | n_inter | 0 | Number of exchange connections with other phases |
| Material properties | |||
| replaceable package Data | Characteristics.BaseClasses…. | Characteristic data | |
| Mobility | mu | sigma*v | Mobility [N.T/M] |
| TimeAbsolute | nu | Data.nu(T, v) | Thermal independity [T] |
| DiffusivityMassSpecific | zeta | Data.zeta(T, v) | ** [L2.M/(N.T)] |
| Fluidity | eta | Data.eta(T, v) | Fluidity [L.T/M] |
| ResistivityThermal | theta | Data.theta(T, v) | Thermal resistivity [L.T/N] |
| ConductivityElectrical | sigma | Data.mu()/Data.v_Tp() | Electrical conductivity [N2.T/(L3.M)] |
| Independence factors | |||
| NumberAbsolute | k_intra_Phi[n_intra, n_trans] | ones(n_intra, n_trans) | For translational exchange among species within the phase [1] |
| NumberAbsolute | k_intra_Q[n_intra] | ones(n_intra) | For thermal exchange among species within the phase [1] |
| Initialization | |||
| Velocity | phi.start[n_trans] | 0 | Velocity [L/T] |
| Current | I.start[n_trans] | 0 | Current [N/T] |
| Velocity | phi_boundaries.start[n_trans, Side] | 0 | Normal velocities at the boundaries [L/T] |
| Force | f.start[n_trans] | 0 | Total normal translational force on pairs of boundaries [L.M/T2] |
| Force | minusDeltaf.start[n_trans] | 0 | Dynamic and nonequilibrium compression forces [L.M/T2] |
| Chemical parameters | |||
| TimeAbsolute | tauprime[n_chem] | zeros(n_chem) | Specific exchange currents [T] |
| Geometry | |||
| Length | kL[:] | L[cartTrans] | Effective transport length [L] |
| Initialization | |||
| Init | initMaterial | Init.pressure | Method of initializing the material state |
| Init | initEnergy | Init.temperature | Method of initializing the thermal state |
| Amount | N_IC | Initial amount of material [N] | |
| Density | rho_IC | Initial density [N/L3] | |
| Volume | V_IC | Initial volume [L3] | |
| PressureAbsolute | p_IC | Initial pressure [M/(L.T2)] | |
| TemperatureAbsolute | T_IC | Initial temperature [L2.M/(N.T2)] | |
| Potential | h_IC | Initial specific enthalpy [L2.M/(N.T2)] | |
| Potential | g_IC | Initial Gibbs potential [L2.M/(N.T2)] | |
| Assumptions | |||
| Integer | n_trans | 1 | Number of transport axes |
| Integer | n_chem | 0 | Number of reaction and phase change processes |
| Formulation of the conservation equations | |||
| ConsThermo | consMaterial | ConsThermo.dynamic | Material |
| Boolean | consRot | false | Conserve rotational momentum |
| ConsTrans | consTransX | ConsTrans.dynamic | X-axis translational momentum |
| ConsTrans | consTransY | ConsTrans.dynamic | Y-axis translational momentum |
| ConsTrans | consTransZ | ConsTrans.dynamic | Z-axis translational momentum |
| ConsThermo | consEnergy | ConsThermo.dynamic | Energy |
| Axes with upstream discretization | |||
| Boolean | upstreamX | true | X |
| Boolean | upstreamY | true | Y |
| Boolean | upstreamZ | true | Z |
| Flow conditions | |||
| Boolean | approxVelocity | true | Calculate normal boundary velocities assuming uniform density |
| NumberAbsolute | Nu_Phi[Axis] | {4,4,4} | Translational Nusselt numbers [1] |
| NumberAbsolute | Nu_Q | 1 | Thermal Nusselt number [1] |
| Advanced | |||
| Amount | N0 | 0 | Nominal amount of material to prevent depletion [N] |
Connectors
| Type | Name | Description |
|---|---|---|
| Intra | intra[n_intra] | Connectors to exchange translational momentum and energy within the phase |
| Inter | inter[n_inter] | Connectors to exchange translational momentum and energy with all other species |
| Dalton | dalton | Connector for additivity of pressure |
| Boundary | boundaries[n_trans, Side] | Connectors for transport |
| Chemical | chemical[n_chem] | Connector for reactions and phase change |
Modelica definition
model Ion "Base model for an ion" import assert = FCSys.Utilities.assertEval; extends Fluid(final mu=sigma*v, N(stateSelect=StateSelect.default)); parameter Q.ConductivityElectrical sigma=Data.mu()/Data.v_Tp() "Electrical conductivity"; end Ion;
 FCSys.Species.Fluid
FCSys.Species.Fluid
Base model for a fluid species

Information
Fixed assumptions:
- The gradient of material current is uniform in the direction of the current.
- The normal translational force on pairs of boundaries is split equally between the boundaries. This includes the body, shear (transverse translational transport), and exchange forces due to intermolecular drag and transfer during chemical reactions and phase change. It excludes the thermodynamic, dynamic (advective normal translational transport), and nonequilibrium (irreversible compression) pressures. It also excludes transient effects since translational momentum is stored at the boundaries (not in the subregion).
- Nonequilibrium pressure is included in the thermodynamic states at the boundaries. In particular, the specific enthalpy at a boundary is a function of the temperature and the sum of the thermodynamic and nonequilibrium pressures at the boundary (and a possible artifact of dynamic pressure; see the first note regarding parameters). The rate of advection of energy is the product of this specific enthalpy and the material current.
Notes regarding the parameters:
- If
approxVelocityistrue, then the normal velocities at the boundaries are calculated from the boundary currents assuming that the density is uniform. This avoids nonlinear systems of equations, but it introduces an artifact of the dynamic pressure into the thermodynamic states at the boundaries. The extra pressure is m Ṅi2 (v - vi)/A′, where m is the specific mass, v is the specific volume in the subregion, vi is the specific volume at the boundary, Ṅi is the boundary current, and A′ is the available cross-sectional area. This affects the energy balance via the specific enthalpy at the boundaries. - If
consTransX,consTransY, orconsTransZisConsTrans.steady, then the derivative of translational momentum at and normal to the boundaries (proportional to ∂Ṅi/∂t) is treated as zero and removed from the translational momentum balances/material transport equations at the corresponding boundaries. - If consRot is
true, then rotational momentum is conserved without storage (i.e., steady). This means that the shear forces are mapped so that there is no net torque around any rotational axis that has all its boundaries included (i.e., all the boundaries around the perimeter). Rotational momentum is not exchanged among species or directly transported (i.e., uniform or shaft rotation). - Upstream discretization is applied by default.
The central difference
scheme may be used by setting
upstreamX,upstreamY, andupstreamZtotrue. The typical diffusion properties are such that the Péclet number for the upstream discretization of pressure will be much less (factor of 1/10,000) than the Péclet numbers for translational and thermal transport. Therefore, it may appear that pressure is not advected with the material transport stream. - The indices of the translational Nusselt number (NuΦ) correspond to the orientation of the translational momentum that is transported, not the axes of material transport.
- The default thermal Nusselt number is one, which represents pure conduction through the gas. Use 3.66 for internal flow where the boundaries are uniform in temperature or 48/11 (approximately 4.36) if the heat flux is uniform [Incropera2002].
Translational momentum and thermal energy are advected as material is exchanged due to phase change and reactions. This occurs at the velocity (φ) and the specific entropy-temperature product (sT) of the reactants (source configurations), where the reactant/product designation depends on the current conditions.
The advective exchange is modeled via a stream connector
(Chemical).
The rate of advection of translational momentum is the
product of the velocity of the source (φ) and the mass flow rate
(Ṁ or mṄ). The rate of thermal advection is the
specific entropy-temperature product of the source (sT) times the rate of
material exchange
(Ṅ). If there are multiple sources, then
their contributions are additive. If there are multiple sinks, then
translational momentum is split on a mass basis and the thermal stream is split
on a particle-number basis.
For more information, please see the Species model.
Extends from Species (Base model for one chemical species in one phase).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Integer | n_inter | 0 | Number of exchange connections with other phases |
| Material properties | |||
| replaceable package Data | Characteristics.BaseClasses…. | Characteristic data | |
| Mobility | mu | Data.mu(T, v) | Mobility [N.T/M] |
| TimeAbsolute | nu | Data.nu(T, v) | Thermal independity [T] |
| DiffusivityMassSpecific | zeta | Data.zeta(T, v) | ** [L2.M/(N.T)] |
| Fluidity | eta | Data.eta(T, v) | Fluidity [L.T/M] |
| ResistivityThermal | theta | Data.theta(T, v) | Thermal resistivity [L.T/N] |
| Independence factors | |||
| NumberAbsolute | k_intra_Phi[n_intra, n_trans] | ones(n_intra, n_trans) | For translational exchange among species within the phase [1] |
| NumberAbsolute | k_intra_Q[n_intra] | ones(n_intra) | For thermal exchange among species within the phase [1] |
| Initialization | |||
| TemperatureAbsolute | T.start | T_IC | Temperature [L2.M/(N.T2)] |
| Velocity | phi.start[n_trans] | 0 | Velocity [L/T] |
| Chemical parameters | |||
| TimeAbsolute | tauprime[n_chem] | zeros(n_chem) | Specific exchange currents [T] |
| Geometry | |||
| Length | kL[:] | L[cartTrans] | Effective transport length [L] |
| Initialization | |||
| Init | initMaterial | Init.pressure | Method of initializing the material state |
| Init | initEnergy | Init.temperature | Method of initializing the thermal state |
| Amount | N_IC | Initial amount of material [N] | |
| Density | rho_IC | Initial density [N/L3] | |
| Volume | V_IC | Initial volume [L3] | |
| PressureAbsolute | p_IC | Initial pressure [M/(L.T2)] | |
| TemperatureAbsolute | T_IC | Initial temperature [L2.M/(N.T2)] | |
| Potential | h_IC | Initial specific enthalpy [L2.M/(N.T2)] | |
| Potential | g_IC | Initial Gibbs potential [L2.M/(N.T2)] | |
| Assumptions | |||
| Integer | n_trans | 1 | Number of transport axes |
| Integer | n_chem | 0 | Number of reaction and phase change processes |
| Formulation of the conservation equations | |||
| ConsThermo | consMaterial | ConsThermo.dynamic | Material |
| Boolean | consRot | false | Conserve rotational momentum |
| ConsTrans | consTransX | ConsTrans.dynamic | X-axis translational momentum |
| ConsTrans | consTransY | ConsTrans.dynamic | Y-axis translational momentum |
| ConsTrans | consTransZ | ConsTrans.dynamic | Z-axis translational momentum |
| ConsThermo | consEnergy | ConsThermo.dynamic | Energy |
| Axes with upstream discretization | |||
| Boolean | upstreamX | true | X |
| Boolean | upstreamY | true | Y |
| Boolean | upstreamZ | true | Z |
| Flow conditions | |||
| Boolean | approxVelocity | true | Calculate normal boundary velocities assuming uniform density |
| NumberAbsolute | Nu_Phi[Axis] | {4,4,4} | Translational Nusselt numbers [1] |
| NumberAbsolute | Nu_Q | 1 | Thermal Nusselt number [1] |
| Advanced | |||
| Amount | N0 | 0 | Nominal amount of material to prevent depletion [N] |
Connectors
| Type | Name | Description |
|---|---|---|
| Intra | intra[n_intra] | Connectors to exchange translational momentum and energy within the phase |
| Inter | inter[n_inter] | Connectors to exchange translational momentum and energy with all other species |
| Dalton | dalton | Connector for additivity of pressure |
| Boundary | boundaries[n_trans, Side] | Connectors for transport |
| Chemical | chemical[n_chem] | Connector for reactions and phase change |
Modelica definition
model Fluid "Base model for a fluid species" import FCSys.Utilities.Coordinates.after; import FCSys.Utilities.Coordinates.before; import FCSys.Utilities.Coordinates.cartWrap; import FCSys.Utilities.Delta; import FCSys.Utilities.Sigma; import FCSys.Utilities.inSign; import FCSys.Utilities.selectBooleans; import FCSys.Utilities.selectIntegers; import assert = FCSys.Utilities.assertEval; // Initialization parameters parameter Init initMaterial=Init.pressure "Method of initializing the material state"; parameter Init initEnergy=Init.temperature "Method of initializing the thermal state"; // Note: The extension is after these parameters so that they appear first // in the parameter dialog. extends Species(N(stateSelect=if consMaterial == ConsThermo.dynamic then StateSelect.always else StateSelect.prefer),T(final fixed=false)); // Note: StateSelect.always isn't ideal, but it's necessary to avoid // dynamic state selection in Dymola 2014. In some cases it isn't // appropriate (e.g., an incompressible liquid that fills the entire // subregion), and in those cases it can be modified at instantiation. // Material properties parameter Integer n_chem=0 "Number of reaction and phase change processes"; Q.DiffusivityMassSpecific zeta(nominal=1e-3*U.N/U.A) = Data.zeta(T, v) "**"; Q.Fluidity eta(nominal=1e5/(U.Pa*U.s)) = Data.eta(T, v) "Fluidity"; Q.ResistivityThermal theta(nominal=10*U.m*U.K/U.W) = Data.theta(T, v) "Thermal resistivity"; // Chemical parameters Q.TimeAbsolute tauprime[n_chem](each nominal=U.ms) = zeros(n_chem) "Specific exchange currents"; // Geometry Q.Length kL[:]=L[cartTrans] "Effective transport length"; // Note: The size is n_trans, but it isn't specified here to // prevent a warning in Dymola 2014. // Assumptions // ----------- // Dynamics parameter ConsThermo consMaterial=ConsThermo.dynamic "Material"; parameter Boolean consRot=false "Conserve rotational momentum"; parameter ConsTrans consTransX=ConsTrans.dynamic "X-axis translational momentum"; parameter ConsTrans consTransY=ConsTrans.dynamic "Y-axis translational momentum"; parameter ConsTrans consTransZ=ConsTrans.dynamic "Z-axis translational momentum"; parameter ConsThermo consEnergy=ConsThermo.dynamic "Energy"; // // Upstream discretization parameter Boolean upstreamX=true "X"; parameter Boolean upstreamY=true "Y"; parameter Boolean upstreamZ=true "Z"; // // Flow conditions parameter Boolean approxVelocity=true "Calculate normal boundary velocities assuming uniform density"; parameter Q.NumberAbsolute Nu_Phi[Axis]={4,4,4} "Translational Nusselt numbers"; parameter Q.NumberAbsolute Nu_Q=1 "Thermal Nusselt number"; // Advanced parameters parameter Q.Amount N0=0 "Nominal amount of material to prevent depletion"; // Aliases (for common terms) Q.Current I[n_trans]( each nominal=U.A, each stateSelect=StateSelect.never, each start=0) "Current"; Q.Velocity phi_boundaries[n_trans, Side]( each nominal=100*U.cm/U.s, each stateSelect=StateSelect.never, each start=0) "Normal velocities at the boundaries"; Q.Force f[n_trans]( each nominal=U.N, each stateSelect=StateSelect.never, each start=0) "Total normal translational force on pairs of boundaries"; // This (f) includes the body, shear, and exchange forces due to // intermolecular drag and transfer during chemical reactions and phase // change. It excludes the thermodynamic, dynamic, and nonequilibrium // compressive forces. It also excludes transient effects since // translational momentum is stored at the boundaries. Q.Force minusDeltaf[n_trans]( each nominal=U.N, each stateSelect=StateSelect.never, each start=0) "Dynamic and nonequilibrium compression forces"; // Auxiliary variables (for analysis) // ---------------------------------- // Misc. conditions output Q.Density rho_boundaries[n_trans, Side](each stateSelect=StateSelect.never) = fill( 1, n_trans, 2) ./ Data.v_Tp(boundaries.T, boundaries.p) if environment.analysis "Densities at the boundaries"; output Q.VolumeRate Vdot_boundaries[n_trans, Side](each stateSelect= StateSelect.never) = boundaries.Ndot ./ rho_boundaries if environment.analysis "Volume flow rates into the boundaries"; output Q.PressureAbsolute q[n_trans](each stateSelect=StateSelect.never) = ( Data.m/2)*phi .* I ./ Aprime if environment.analysis "Dynamic pressure"; output Q.Velocity phi_chemical[n_chem, n_trans](each stateSelect=StateSelect.never) = actualStream(chemical.phi) if environment.analysis and n_chem > 0 "Velocity of the chemical streams"; output Q.PotentialAbsolute sT_chemical[n_chem](each stateSelect=StateSelect.never) = actualStream(chemical.sT) if environment.analysis and n_chem > 0 "Specific entropy-temperature product of the chemical streams"; output Q.Temperature DeltaT[n_trans](each stateSelect=StateSelect.never) = Delta(boundaries.T) if environment.analysis "Differences in temperatures across the boundaries"; output Q.Pressure Deltap[n_trans](each stateSelect=StateSelect.never) = Delta (boundaries.p) if environment.analysis "Differences in pressures across the boundaries"; output Q.Power Hprimedot[n_trans, Side](each stateSelect=StateSelect.never) = (Data.h(boundaries.T, boundaries.p) + Data.m*phi_boundaries .^ 2/2) .* boundaries.Ndot if environment.analysis "Flow rates of enthalpy + kinetic energy into the boundaries"; // // Potentials output Q.Potential g_boundaries[n_trans, Side](each stateSelect=StateSelect.never) = Data.g(boundaries.T, boundaries.p) if environment.analysis and not Data.isCompressible "Gibbs potentials at the boundaries"; output Q.Potential Deltag[n_trans](each stateSelect=StateSelect.never) = Delta(g_boundaries) if environment.analysis and not Data.isCompressible "Differences in Gibbs potentials across the boundaries"; // Note: If a boundary is left unconnnected, then it's possible that its // pressure may become negative. If the equation of state has an ideal-gas // term, then the Gibbs energy will involve a logarithm of pressure. // Therefore, to prevent errors, these variables are included only for // incompressible species. // // Time constants output Q.TimeAbsolute tau_NT[n_trans]( each stateSelect=StateSelect.never, each start=U.s) = fill(zeta*beta*N, n_trans) ./ (2*Aprime) if environment.analysis "Time constants for material transport"; output Q.TimeAbsolute tau_PhiT[n_trans]( each stateSelect=StateSelect.never, each start=U.s) = M*eta*kL ./ (2*Nu_Phi[cartTrans] .* Aprime) if environment.analysis "Time constants for transverse translational transport"; output Q.TimeAbsolute tau_QT[n_trans]( each stateSelect=StateSelect.never, each start=U.s) = (N*c_v*theta/(2*Nu_Q))*kL ./ Aprime if environment.analysis "Time constants for thermal transport"; // // Peclet numbers output Q.Number Pe_N[n_trans](each stateSelect=StateSelect.never) = tau_NT .* I/N if environment.analysis "Material Peclet numbers"; output Q.Number Pe_Phi[n_trans](each stateSelect=StateSelect.never) = tau_PhiT .* I/N if environment.analysis "Translational Peclet numbers"; output Q.Number Pe_Q[n_trans](each stateSelect=StateSelect.never) = tau_QT .* I/N if environment.analysis "Thermal Peclet numbers"; // Note: These Peclet numbers are calculated at the center of the // subregion (for simplicity), but the Peclet numbers used in the transport // equations are at each boundary. // // Bulk flow rates output Q.Force mphiI[n_trans, n_trans](each stateSelect=StateSelect.never) = outerProduct(I, Data.m*phi) if environment.analysis "Bulk rate of translational advection (1st index: transport axis, 2nd index: translational component)"; output Q.VolumeRate Vdot[n_trans](each stateSelect=StateSelect.never) = v*I if environment.analysis "Bulk volumetric flow rate"; output Q.Power hI[n_trans](each stateSelect=StateSelect.never) = h*I if environment.analysis "Bulk enthalpy flow rate"; // // Translational momentum balance output Q.Force Ma[n_trans](each stateSelect=StateSelect.never) = M*(der(phi)/ U.s + environment.a[cartTrans]) + N*Data.z*environment.E[cartTrans] if environment.analysis "Acceleration force (including acceleration due to body forces)"; output Q.Force f_thermo[n_trans](each stateSelect=StateSelect.never) = -Delta (boundaries.p) .* Aprime if environment.analysis "Thermodynamic force"; output Q.Force f_AE[n_trans](each stateSelect=StateSelect.never) = Data.m*sum ((actualStream(chemical[i].phi) - phi)*chemical[i].Ndot for i in 1:n_chem) if environment.analysis "Acceleration force due to advective exchange"; output Q.Force f_AT[n_trans](each stateSelect=StateSelect.never) = {sum(((if i == j then phi_boundaries[j, :] else boundaries[j, :].phi[cartWrap( cartTrans[i] - cartTrans[j])]) - {phi[i],phi[i]})*boundaries[j, :].Ndot* Data.m for j in 1:n_trans) for i in 1:n_trans} if environment.analysis "Acceleration force due to advective transport"; output Q.Force f_DT[n_trans](each stateSelect=StateSelect.never) = {sum(sum( if i == j then {0,0} else boundaries[j, :].mPhidot[cartWrap(cartTrans[i] - cartTrans[j])]) for j in 1:n_trans) for i in 1:n_trans} if environment.analysis "Shear force from other subregions (diffusive transport)"; // // Energy balance output Q.Power Ndere(stateSelect=StateSelect.never) = (N*T*der(Data.s(T, p)) + M*phi*der(phi))/U.s if environment.analysis "Rate of energy storage (internal and kinetic) and boundary work at constant mass"; // Note that T*der(s) = der(u) + p*der(v). output Q.Power Edot_AE(stateSelect=StateSelect.never) = sum((chemical[i].g + actualStream(chemical[i].sT) - h + (actualStream(chemical[i].phi)* actualStream(chemical[i].phi) - phi*phi)*Data.m/2)*chemical[i].Ndot for i in 1:n_chem) if environment.analysis "Relative rate of energy (internal, flow, and kinetic) due to reactions and phase change"; output Q.Power Edot_AT(stateSelect=StateSelect.never) = sum((Data.h( boundaries[i, :].T, boundaries[i, :].p) - {h,h} + (phi_boundaries[i, :] .^ 2 + sum(boundaries[i, :].phi[orient] .^ 2 for orient in Orient) - fill(phi* phi, 2))*(Data.m/2))*boundaries[i, :].Ndot for i in 1:n_trans) if environment.analysis "Relative rate of energy (internal, flow, and kinetic) due to advective transport"; output Q.Power Edot_DT(stateSelect=StateSelect.never) = sum(sum(boundaries[i, :].phi[orient]*boundaries[i, :].mPhidot[orient] for orient in Orient) for i in 1:n_trans) + sum(boundaries.Qdot) if environment.analysis "Rate of diffusion of energy from other subregions"; // Note: The structure of the problem shouldn't change if these // auxiliary variables are included (hence, StateSelect.never). Connectors.Boundary boundaries[n_trans, Side]( each p(start=p_IC), each T(start=T_IC), Ndot(each start=0, each stateSelect=StateSelect.never)) "Connectors for transport"; Connectors.Chemical chemical[n_chem]( each final n_trans=n_trans, g(each start=g_IC, each final fixed=false), sT(each start=h_IC - g_IC, each final fixed=false)) "Connector for reactions and phase change"; // Geometric parameters protected outer Q.Area Aprime[n_trans] "Effective cross-sectional area"; outer parameter Boolean inclRot[3] "true, if each axis of rotation has all its tangential boundaries included"; outer parameter Boolean inclTrans[3] "true, if each transport axis is included"; // Note: The size of inclRot and inclTrans is also Axis, but it can't be // specified here due to an error in Dymola 2014. outer parameter Integer cartRot[:] "Cartesian-axis indices of the components of rotational momentum"; // Note: The size of cartRot is n_trans, but it can't be // specified here due to an error in Dymola 2014. outer parameter Integer transCart[3] "Boundary-pair indices of the Cartesian axes"; // Note: The size is also Axis, but it can't be specified here due // to an error in Dymola 2014. final parameter ConsTrans consTrans[n_trans]=selectIntegers({consTransX, consTransY,consTransZ}, cartTrans) "Formulation of the translational conservation equations for the transport axes"; final parameter Boolean upstream[n_trans]=selectBooleans({upstreamX,upstreamY, upstreamZ}, cartTrans) "true, if each transport axis uses upstream discretization"; // Additional aliases (for common terms) Q.Force mPhidot_boundaries[n_trans, Side, Orient](each nominal=U.N, each stateSelect=StateSelect.never) "Directly-calculated shear forces"; outer Conditions.Environment environment "Environmental conditions"; initial equation // Check the initial conditions. assert(V >= 0, "The volume of " + getInstanceName() + " is negative. Check that the volumes of the other phases are set properly."); assert(initMaterial <> initEnergy or initMaterial == Init.none or consMaterial == ConsThermo.steady or consEnergy == ConsThermo.steady, "The initialization methods for material and energy must be different (unless none)."); // Material if consMaterial == ConsThermo.IC then // Ensure that a condition is selected since the state is prescribed. assert(initMaterial <> Init.none, "The material state of " + getInstanceName() + " is prescribed, yet its condition is not defined. Choose any condition besides none."); elseif consMaterial == ConsThermo.dynamic then // Initialize since there's a time-varying state. if initMaterial == Init.amount then N = N_IC; elseif initMaterial == Init.amountSS then der(N) = 0; elseif initMaterial == Init.density then assert(Data.isCompressible or Data.hasThermalExpansion, getInstanceName() + " is isochoric, yet its material initial condition is based on density."); 1/v = rho_IC; elseif initMaterial == Init.densitySS then assert(Data.isCompressible or Data.hasThermalExpansion, getInstanceName() + " is isochoric, yet its material initial condition is based on density."); der(1/v) = 0; elseif initMaterial == Init.volume then V = V_IC; elseif initMaterial == Init.volumeSS then der(V) = 0; elseif initMaterial == Init.pressure then p = p_IC; assert(Data.isCompressible, getInstanceName() + " is incompressible, yet its material initial condition is based on pressure."); elseif initMaterial == Init.pressureSS then der(p) = 0; assert(Data.isCompressible, getInstanceName() + " is incompressible, yet its material initial condition is based on pressure."); elseif initMaterial == Init.temperature then T = T_IC; elseif initMaterial == Init.temperatureSS then der(T) = 0; elseif initMaterial == Init.specificEnthalpy then h = h_IC; elseif initMaterial == Init.specificEnthalpySS then der(h) = 0; elseif initMaterial == Init.Gibbs then g = g_IC; elseif initMaterial == Init.GibbsSS then der(g) = 0; // Else, there's no initial equation since // initMaterial == Init.none or // consMaterial == ConsThermo.steady. end if; end if; // Energy if consEnergy == ConsThermo.IC then // Ensure that a condition is selected since the state is prescribed. assert(initEnergy <> Init.none, "The energy state of " + getInstanceName() + " is prescribed, yet its condition is not defined. Choose any condition besides none."); elseif consEnergy == ConsThermo.dynamic then // Initialize since there's a time-varying state. if initEnergy == Init.amount then N = N_IC; elseif initEnergy == Init.amountSS then der(N) = 0; elseif initEnergy == Init.density then 1/v = rho_IC; assert(Data.isCompressible or Data.hasThermalExpansion, getInstanceName() + " is isochoric, yet its thermal initial condition is based on density."); elseif initEnergy == Init.densitySS then der(1/v) = 0; assert(Data.isCompressible or Data.hasThermalExpansion, getInstanceName() + " is isochoric, yet its thermal initial condition is based on density."); elseif initEnergy == Init.volume then V = V_IC; elseif initEnergy == Init.volumeSS then der(V) = 0; elseif initEnergy == Init.pressure then p = p_IC; assert(Data.isCompressible, getInstanceName() + " is incompressible, yet its thermal initial condition is based on pressure."); elseif initEnergy == Init.pressureSS then der(p) = 0; assert(Data.isCompressible, getInstanceName() + " is incompressible, yet its thermal initial condition is based on pressure."); elseif initEnergy == Init.temperature then T = T_IC; elseif initEnergy == Init.temperatureSS then der(T) = 0; elseif initEnergy == Init.specificEnthalpy then h = h_IC; elseif initEnergy == Init.specificEnthalpySS then der(h) = 0; elseif initEnergy == Init.Gibbs then g = g_IC; elseif initEnergy == Init.GibbsSS then der(g) = 0; // Else, there's no initial equation since // initEnergy == Init.none or // consEnergy == ConsThermo.steady. end if; end if; equation // Aliases (only to clarify and simplify other equations) v*I = Aprime .* phi "Current vs. velocity"; for i in 1:n_trans loop for side in Side loop (if approxVelocity then v else Data.v_Tp(boundaries[i, side].T, boundaries[i, side].p))*boundaries[i, side].Ndot = inSign(side)*Aprime[ i]*phi_boundaries[i, side] "Current vs. velocity at the boundaries"; end for; end for; minusDeltaf = Data.m*phi .* I; // Assumptions 2*I = -Delta(boundaries.Ndot) "Linear current profile (assumption #1)"; // Equation of state if Data.isCompressible then p = Data.p_Tv(T, v) + zeta*der(1/v)/U.s; else v = Data.v_Tp(T, p - zeta*der(1/v)/U.s); end if; // Properties upon outflow due to reaction and phase change chemical.phi = fill(phi, n_chem); chemical.sT = fill(h - g, n_chem); // Material exchange for i in 1:n_chem loop if tauprime[i] > Modelica.Constants.small then tauprime[i]*(chemical[i].Ndot - 0.001*der(chemical[i].Ndot)/U.s) = (N + N0)*exp((chemical[i].g - g)/T) - N; else chemical[i].g = g; end if; end for; // Transport for i in 1:n_trans loop for side in Side loop // Material (if consTrans[i] == ConsTrans.dynamic then kL[i]*Data.m*der(boundaries[i, side].Ndot)/U.s else 0) = (Aprime[i]*(boundaries[i, side].p - p) + inSign(side)*Data.m*phi_boundaries[i, side]*boundaries[i, side].Ndot - minusDeltaf[i])*(if upstream[i] then 1 + exp(-zeta*Data.beta(T, p)* boundaries[i, side].Ndot/(2*Aprime[i])) else 2) + inSign(side)*f[i]; // Translational momentum kL[i]*eta*mPhidot_boundaries[i, side, Orient.after] = Aprime[i]*Nu_Phi[ after(cartTrans[i])]*(boundaries[i, side].phi[Orient.after] - (if inclTrans[after(cartTrans[i])] then phi[transCart[after(cartTrans[i])]] else 0))*(if upstream[i] then 1 + exp(-kL[i]*eta*Data.m*boundaries[i, side].Ndot/(2*Aprime[i]*Nu_Phi[after(cartTrans[i])])) else 2) "1st transverse"; kL[i]*eta*mPhidot_boundaries[i, side, Orient.before] = Aprime[i]*Nu_Phi[ before(cartTrans[i])]*(boundaries[i, side].phi[Orient.before] - (if inclTrans[before(cartTrans[i])] then phi[transCart[before(cartTrans[i])]] else 0))*(if upstream[i] then 1 + exp(-kL[i]*eta*Data.m*boundaries[i, side].Ndot/(2*Aprime[i]*Nu_Phi[before(cartTrans[i])])) else 2) "2nd transverse"; // Thermal energy kL[i]*theta*boundaries[i, side].Qdot = Aprime[i]*Nu_Q*(boundaries[i, side].T - T)*(if upstream[i] then 1 + exp(-kL[i]*theta*Data.c_v(T, p)* boundaries[i, side].Ndot/(2*Aprime[i]*Nu_Q)) else 2); end for; // Direct mapping of shear forces (calculated above) if not (consRot and inclRot[before(cartTrans[i])]) then boundaries[i, :].mPhidot[Orient.after] = mPhidot_boundaries[i, :, Orient.after]; // Else, the force must be mapped for zero torque (below). end if; if not (consRot and inclRot[after(cartTrans[i])]) then boundaries[i, :].mPhidot[Orient.before] = mPhidot_boundaries[i, :, Orient.before]; // Else, the force must be mapped for zero torque (below). end if; end for; // Zero-torque mapping of shear forces if consRot then for axis in cartRot loop 4*cat( 1, boundaries[transCart[after(axis)], :].mPhidot[Orient.after], boundaries[transCart[before(axis)], :].mPhidot[Orient.before]) = {{3,1, L[before(axis)]/L[after(axis)],-L[before(axis)]/L[after(axis)]},{1,3,-L[ before(axis)]/L[after(axis)],L[before(axis)]/L[after(axis)]},{L[after( axis)]/L[before(axis)],-L[after(axis)]/L[before(axis)],3,1},{-L[after( axis)]/L[before(axis)],L[after(axis)]/L[before(axis)],1,3}}*cat( 1, mPhidot_boundaries[transCart[after(axis)], :, Orient.after], mPhidot_boundaries[transCart[before(axis)], :, Orient.before]); end for; end if; // Material dynamics if consMaterial == ConsThermo.IC then // Apply the IC forever (material not conserved). if initMaterial == Init.amount then N = N_IC; elseif initMaterial == Init.amountSS then der(N) = 0; elseif initMaterial == Init.density then 1/v = rho_IC; elseif initMaterial == Init.densitySS then der(1/v) = 0; elseif initMaterial == Init.volume then V = V_IC; elseif initMaterial == Init.volumeSS then der(V) = 0; elseif initMaterial == Init.pressure then p = p_IC; elseif initMaterial == Init.pressureSS then der(p) = 0; elseif initMaterial == Init.temperature then T = T_IC; elseif initMaterial == Init.temperatureSS then der(T) = 0; elseif initMaterial == Init.specificEnthalpy then h = h_IC; elseif initMaterial == Init.specificEnthalpySS then der(h) = 0; elseif initMaterial == Init.Gibbs then g = g_IC; else // if initMaterial == Init.GibbsSS then der(g) = 0; // Note: initMaterial == Init.none can't occur due to an assertion. end if; else (if consMaterial == ConsThermo.dynamic then der(N)/U.s else 0) = sum( chemical.Ndot) + sum(boundaries.Ndot) "Material conservation"; end if; // Conservation of translational momentum f + M*environment.a[cartTrans] + Data.z*N*environment.E[cartTrans] = Data.m* sum(actualStream(chemical[i].phi)*chemical[i].Ndot for i in 1:n_chem) + { sum(intra[:].mPhidot[j]) + sum(inter[:].mPhidot[j]) + sum((if i == j then 0 else boundaries[i, :].phi[cartWrap(cartTrans[j] - cartTrans[i])]* boundaries[i, :].Ndot*Data.m + sum(boundaries[i, :].mPhidot[cartWrap( cartTrans[j] - cartTrans[i])])) for i in 1:n_trans) for j in 1:n_trans}; // Note: The storage is split between the boundaries via f, so a // derivative doesn't appear here (see material transport above). // Note: The explicit expansions (intra[:] and inter[:]) are necessary in // Dymola 2014. // Thermal dynamics if consEnergy == ConsThermo.IC then // Apply the IC forever (energy not conserved). if initEnergy == Init.amount then N = N_IC; elseif initEnergy == Init.amountSS then der(N) = 0; elseif initEnergy == Init.density then 1/v = rho_IC; elseif initEnergy == Init.densitySS then der(1/v) = 0; elseif initEnergy == Init.volume then V = V_IC; elseif initEnergy == Init.volumeSS then der(V) = 0; elseif initEnergy == Init.pressure then p = p_IC; elseif initEnergy == Init.pressureSS then der(p) = 0; elseif initEnergy == Init.temperature then T = T_IC; elseif initEnergy == Init.temperatureSS then der(T) = 0; elseif initEnergy == Init.specificEnthalpy then h = h_IC; elseif initEnergy == Init.specificEnthalpySS then der(h) = 0; elseif initEnergy == Init.Gibbs then g = g_IC; else // if initEnergy == Init.GibbsSS then der(g) = 0; // Note: initEnergy == Init.none can't occur due to an assertion. end if; else (if consEnergy == ConsThermo.dynamic then (N*T*der(s) + der(M*phi*phi)/2)/U.s else 0) = sum((chemical[i].g + actualStream(chemical[i].sT) - h + actualStream(chemical[i].phi)*actualStream(chemical[i].phi)*Data.m/2)* chemical[i].Ndot for i in 1:n_chem) + sum(intra[i].phi*intra[i].mPhidot for i in 1:n_intra) + sum(inter[i].phi*inter[i].mPhidot for i in 1: n_inter) + sum(intra.Qdot) + sum(inter.Qdot) + sum((Data.h(boundaries[i, :].T, boundaries[i, :].p) - {h,h} + (phi_boundaries[i, :] .^ 2 + sum( boundaries[i, :].phi[orient] .^ 2 for orient in Orient))*(Data.m/2))* boundaries[i, :].Ndot + sum(boundaries[i, :].phi[orient]*boundaries[i, :].mPhidot[ orient] for orient in Orient) for i in 1:n_trans) + sum(boundaries.Qdot) "Conservation of energy"; end if; end Fluid;
 FCSys.Species.Solid
FCSys.Species.Solid
Base model for an inert, stationary solid

Information
Assumptions:
- There is no material transport.
- Velocity is zero.
- There are no chemical reactions or phase change.
- The volume is constant—determined by ε and the total volume of the subregion.
For more information, please see the Species model.
Extends from Species (Base model for one chemical species in one phase).
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Integer | n_inter | 0 | Number of exchange connections with other phases |
| Geometry | |||
| NumberAbsolute | epsilon | 0.25 | Volumetric fill fraction [1] |
| Length | kL[:] | L[cartTrans] | Effective transport length [L] |
| Material properties | |||
| replaceable package Data | Characteristics.BaseClasses…. | Characteristic data | |
| Mobility | mu | Data.mu(T, v) | Mobility [N.T/M] |
| TimeAbsolute | nu | Data.nu(T, v) | Thermal independity [T] |
| ResistivityThermal | theta | Data.theta(T, v) | Thermal resistivity [L.T/N] |
| Independence factors | |||
| NumberAbsolute | k_intra_Phi[n_intra, n_trans] | ones(n_intra, n_trans) | For translational exchange among species within the phase [1] |
| NumberAbsolute | k_intra_Q[n_intra] | ones(n_intra) | For thermal exchange among species within the phase [1] |
| Initialization | |||
| TemperatureAbsolute | T.start | T_IC | Temperature [L2.M/(N.T2)] |
| Velocity | phi.start[n_trans] | 0 | Velocity [L/T] |
| Assumptions | |||
| Integer | n_trans | 1 | Number of transport axes |
| Formulation of the conservation equations | |||
| ConsThermo | consEnergy | ConsThermo.dynamic | Energy |
| Initialization | |||
| Density | rho_IC | 1/Data.v_Tp() | Initial density [N/L3] |
| Volume | V_IC | epsilon*product(L) | Initial volume [L3] |
| PressureAbsolute | p_IC | environment.p | Initial pressure [M/(L.T2)] |
| TemperatureAbsolute | T_IC | Initial temperature [L2.M/(N.T2)] | |
Connectors
| Type | Name | Description |
|---|---|---|
| Intra | intra[n_intra] | Connectors to exchange translational momentum and energy within the phase |
| Inter | inter[n_inter] | Connectors to exchange translational momentum and energy with all other species |
| Dalton | dalton | Connector for additivity of pressure |
| ThermalDiffusive | boundaries[n_trans, Side] | Connectors for transport |
Modelica definition
model Solid "Base model for an inert, stationary solid" import FCSys.Utilities.Delta; // Geometry parameter Q.NumberAbsolute epsilon=0.25 "Volumetric fill fraction"; extends Species( final N_IC, final V_IC=epsilon*product(L), final rho_IC=1/Data.v_Tp(), final p_IC=environment.p, final h_IC, final g_IC, T(stateSelect=if consEnergy == ConsThermo.dynamic then StateSelect.always else StateSelect.default,fixed=consEnergy == ConsThermo.dynamic)); parameter Q.Length kL[:]=L[cartTrans] "Effective transport length"; // Note: The size is n_trans, but it isn't specified here to prevent a // warning in Dymola 2014. // Material properties Q.ResistivityThermal theta(nominal=10*U.cm/U.A) = Data.theta(T, v) "Thermal resistivity"; // Assumptions parameter ConsThermo consEnergy=ConsThermo.dynamic "Energy"; // Auxiliary variables (for analysis) output Q.TimeAbsolute tau_QT[n_trans]( each stateSelect=StateSelect.never, each start=U.s) = N*c_v*theta*kL ./ (2*Aprime) if environment.analysis "Time constants for thermal transport (through the whole subregion)"; output Q.Temperature DeltaT[n_trans](each stateSelect=StateSelect.never) = Delta(boundaries.T) if environment.analysis "Differences in temperatures across the boundaries"; Connectors.ThermalDiffusive boundaries[n_trans, Side](T(each start=T_IC)) "Connectors for transport"; protected outer Q.Area Aprime[n_trans] "Effective cross-sectional area"; equation // Assumptions phi = zeros(n_trans) "Zero velocity"; V = epsilon*product(L) "Prescribed volume"; // Equation of state if Data.isCompressible then p = Data.p_Tv(T, v); else v = Data.v_Tp(T, p); end if; // Thermal transport (conduction) for i in 1:n_trans loop for side in Side loop kL[i]*theta*boundaries[i, side].Qdot = 2*Aprime[i]*(boundaries[i, side].T - T); end for; end for; // Thermal dynamics if consEnergy == ConsThermo.IC then // Apply the IC forever (energy not conserved). T = T_IC; else (if consEnergy == ConsThermo.dynamic then N*T*der(s)/U.s else 0) = sum( intra[i].phi*intra[i].mPhidot for i in 1:n_intra) + sum(inter[i].phi* inter[i].mPhidot for i in 1:n_inter) + sum(intra.Qdot) + sum(inter.Qdot) + sum(boundaries.Qdot) "Conservation of energy"; end if; end Solid;
 FCSys.Species.Species
FCSys.Species.Species
Base model for one chemical species in one phase

Information
All of the details below are pertinent to the Fluid model (and the derived Ion model) which inherits from this model. Only some of the details apply to the Solid model because it excludes the transport and exchange of material.
This model is based on the following fixed assumptions:
- All boundaries are rectangular.
- The material is orthorhombic. This implies that a gradient which induces diffusion along an axis does not induce diffusion along axes orthogonal to it [Bejan2006, pp. 691–692].
- The coordinate system (x, y, z) is aligned with the principle axes of transport. For example, if the material is stratified, then the layers must be parallel to one of the planes in the rectilinear grid.
- The effective transport lengths (kL) are common to material, translational, and thermal transport.
- There is no radiative heat transfer (or it must be linearized and added to the thermal conductance).
- Rotational momentum is not stored or transfered.
Figure 1 shows how instances of Species models are connected within a Subregion. A single species in a single phase is called a configuration. The generalized resistances (R) affect the force and rates of chemical exchange and heat flow associated with differences in activity, velocity, and temperature (respectively) between each configuration and a common node. These exchange processes are diffusive. Each resistor generates heat in the Species instance that contains it.
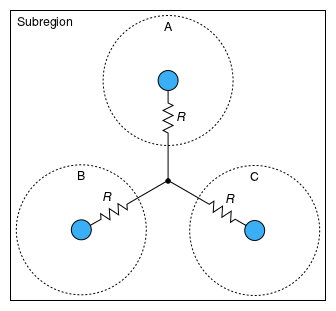
Figure 1: Exchange of a quantity (material, translational momentum, or thermal energy) among configurations
(A, B, and C) within a subregion.
Figure 2 shows how
a configuration
is connected between neighboring instances of a
Subregion.
Material, translational momentum, and thermal energy are transported by both advection and diffusion.
Upstream discretization is applied if it is enabled via the upstreamX,
etc. parameters. Like for exchange, the transport resistances are inside the
Species model.
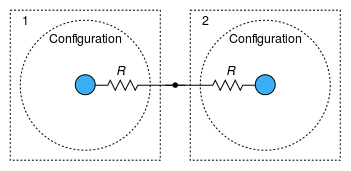
Figure 2: Transport of a quantity associated with the same configuration
between subregions (1 and 2).
The Species instances within a Phase are combined by Dalton's law of partial pressures (see the Dalton connector), as shown in Figure 3a. The pressures are additive, and each species is assumed to exist at the total extensive volume of the phase. Within a Subregion, the Phases are combined by Amagat's law of partial volumes (see the Amagat connector), as shown in Figure 3b. The volumes are additive, and each species is assumed to exist at the total pressure in the subregion.
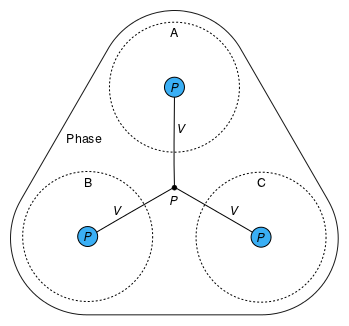
a: Pressures of species (A, B, and C) are additive within a phase. |
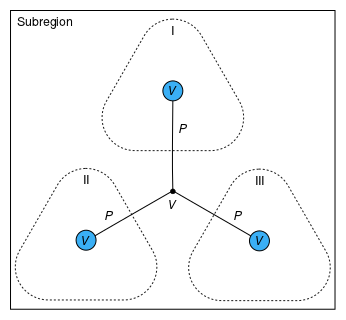
b: Volumes of phases (I, II, and III) are additive within a subregion. |
| Figure 3: Methods of attributing pressure and volume. | |
Notes regarding the parameters:
- The effective transport lengths (kL) may be different that the geometric lengths along the transport axes due to tortouisity. The tortouisity may be anisotropic.
- If the interval for chemical exchange (τ′), mobility (μ),
thermal independity (ν), fluidity (η), or thermal resistivity (θ)
is zero, then
it should usually be set as
finalso that index reduction may be performed. If two configurations are connected through theirintra,inter, orboundariesconnectors and both have zero generalized resistivities for a quantity, then index reduction [Mattsson1993] is necessary. - Even if an initialization parameter is not selected for explicit use, it may be used a guess value.
- If
ConsThermo.ICis used for a state (viaconsMaterialorconsEnergy), then the associated initial condition (IC) will be applied forever instead of the corresponding conservation equation. - If
consEnergyisConsThermo.steady, then NT∂s/∂t + Mφ∂φ/∂t is treated as zero and removed from the energy balance. - If a transport axis is not included (via the outer
inclTrans[:]parameter which maps to{inclTransX, inclTransY, inclTransZ}in the Subregion model), then the associated pair of boundaries is removed from the model. - The
startvalues of the initial conditions for pressure and temperature (pIC and TIC) are the global default pressure and temperature (via theouterinstance of the Environment model). Thestartvalues of the initial conditions for other intensive properties (ρIC, hIC, and gIC) are related to the initial pressure and temperature by the characteristics of the species. Thestartvalue of the initial condition for the extensive volume (VIC) is the volume of the subregion. Thestartvalue for particle number (NIC) is related to it via the material characteristics and the initial pressure and temperature. In order to apply other values for any of these initial conditions, it may be necessary to do so before translating the model.
In the boundaries connector array, the transverse translational flow (mΦdot) is only the
force due to diffusion. Translational advection is calculated from the current and the velocity.
The thermal flow (Q̇) is only the rate of heat transfer due to diffusion. The advection of
thermal energy is determined from the current and the thermodynamic state at the boundary.
For the variables that relate to transport, the first index is the axis and the second index is the side. The sides are ordered from negative to positive, according to the Side enumeration. Velocity and force are additionally indexed by the orientation of the momentum with respect to the boundary. The orientations are ordered following the normal axis in Cartesian space, according to the Orient enumeration.
Parameters
| Type | Name | Default | Description |
|---|---|---|---|
| Integer | n_inter | 0 | Number of exchange connections with other phases |
| Material properties | |||
| replaceable package Data | Characteristics.BaseClasses…. | Characteristic data | |
| Mobility | mu | Data.mu(T, v) | Mobility [N.T/M] |
| TimeAbsolute | nu | Data.nu(T, v) | Thermal independity [T] |
| Independence factors | |||
| NumberAbsolute | k_intra_Phi[n_intra, n_trans] | ones(n_intra, n_trans) | For translational exchange among species within the phase [1] |
| NumberAbsolute | k_intra_Q[n_intra] | ones(n_intra) | For thermal exchange among species within the phase [1] |
| Assumptions | |||
| Integer | n_trans | 1 | Number of transport axes |
| Initialization | |||
| Amount | N_IC | Initial amount of material [N] | |
| Density | rho_IC | Initial density [N/L3] | |
| Volume | V_IC | Initial volume [L3] | |
| PressureAbsolute | p_IC | Initial pressure [M/(L.T2)] | |
| TemperatureAbsolute | T_IC | Initial temperature [L2.M/(N.T2)] | |
| Potential | h_IC | Initial specific enthalpy [L2.M/(N.T2)] | |
| Potential | g_IC | Initial Gibbs potential [L2.M/(N.T2)] | |
Connectors
| Type | Name | Description |
|---|---|---|
| Intra | intra[n_intra] | Connectors to exchange translational momentum and energy within the phase |
| Inter | inter[n_inter] | Connectors to exchange translational momentum and energy with all other species |
| Dalton | dalton | Connector for additivity of pressure |
| Material properties | ||
| replaceable package Data | Characteristic data | |
Modelica definition
partial model Species "Base model for one chemical species in one phase" import assert = FCSys.Utilities.assertEval; // Material properties replaceable package Data = Characteristics.BaseClasses.Characteristic constrainedby Characteristics.BaseClasses.Characteristic "Characteristic data"; Q.Mobility mu(nominal=10*U.cm^2/(U.V*U.s)) = Data.mu(T, v) "Mobility"; Q.TimeAbsolute nu(nominal=1e-9*U.s) = Data.nu(T, v) "Thermal independity"; // Assumptions parameter Integer n_trans=1 "Number of transport axes"; // This can't be an outer parameter in Dymola 2014. parameter Integer n_intra=0 "Number of exchange connections within the phase"; parameter Integer n_inter=0 "Number of exchange connections with other phases"; // Initialization parameters parameter Q.Amount N_IC(start=V_IC*rho_IC) "Initial amount of material"; parameter Q.Density rho_IC(start=1/Data.v_Tp(T_IC, p_IC)) "Initial density"; parameter Q.Volume V_IC(start=product(L)) "Initial volume"; parameter Q.PressureAbsolute p_IC(start=environment.p) "Initial pressure"; parameter Q.TemperatureAbsolute T_IC(start=environment.T) "Initial temperature"; parameter Q.Potential h_IC(start=Data.h(T_IC, p_IC), displayUnit="kJ/mol") "Initial specific enthalpy"; parameter Q.Potential g_IC(start=Data.g(T_IC, p_IC), displayUnit="kJ/mol") "Initial Gibbs potential"; // Independence factors parameter Q.NumberAbsolute k_intra_Phi[n_intra, n_trans]=ones(n_intra, n_trans) "For translational exchange among species within the phase"; parameter Q.NumberAbsolute k_intra_Q[n_intra]=ones(n_intra) "For thermal exchange among species within the phase"; // Preferred states // Note: The start values for these variable aren't fixed because the // initial equation section will be used instead. Q.Amount N( final min=Modelica.Constants.small, nominal=4*U.C, final start=N_IC, final fixed=false, stateSelect=StateSelect.prefer) "Amount of material"; Q.TemperatureAbsolute T( nominal=300*U.K, final start=T_IC, stateSelect=StateSelect.prefer) "Temperature"; Q.Velocity phi[n_trans]( each nominal=100*U.cm/U.s, each start=0, each stateSelect=StateSelect.prefer) "Velocity"; // Aliases (for common terms) // Note: StateSelect.never helps avoid dynamic state selection of these // variables in Dymola 2014. Q.PressureAbsolute p( nominal=U.atm, final start=p_IC, final fixed=false, stateSelect=StateSelect.never) "Pressure"; Q.Potential g( nominal=U.V, final start=g_IC, final fixed=false, stateSelect=StateSelect.never) "Specific Gibbs energy"; Q.Mass M( nominal=1e-3*U.g, final start=Data.m*N_IC, stateSelect=StateSelect.never) "Mass"; Q.VolumeSpecific v( nominal=U.cc/(4*U.C), final start=1/rho_IC, final fixed=false, stateSelect=StateSelect.never) "Specific volume"; Q.Potential h( nominal=U.V, final start=h_IC, final fixed=false, stateSelect=StateSelect.never) "Specific enthalpy"; Q.NumberAbsolute s( nominal=25, final start=(h_IC - g_IC)/T_IC, stateSelect=StateSelect.never) "Specific entropy"; // Auxiliary variables (for analysis) // ---------------------------------- // Thermodynamic properties output Q.Density rho(stateSelect=StateSelect.never) = 1/v if environment.analysis "Density"; output Q.MassVolumic mrho(stateSelect=StateSelect.never) = Data.m*rho if environment.analysis "Volumic mass"; output Q.Amount S(stateSelect=StateSelect.never) = N*s if environment.analysis "Entropy"; output Q.CapacityThermalSpecific c_p(stateSelect=StateSelect.never) = Data.c_p(T, p) if environment.analysis "Isobaric specific heat capacity"; output Q.CapacityThermalSpecific c_v(stateSelect=StateSelect.never) = Data.c_v(T, p) if environment.analysis "Isochoric specific heat capacity"; output Q.PressureReciprocal beta(stateSelect=StateSelect.never) = Data.beta(T, p) if environment.analysis "Isothermal compressibility"; // // Time constants output Q.TimeAbsolute tau_PhiE_intra[n_intra, n_trans]( each stateSelect=StateSelect.never, each start=U.s) = {Data.m*mu*k_intra_Phi[i, :] for i in 1:n_intra} if environment.analysis and n_intra > 0 "Time constants for translational intra-phase exchange"; output Q.TimeAbsolute tau_PhiE_inter[n_inter, n_trans]( each stateSelect=StateSelect.never, each start=U.s) = {Data.m*mu*k_inter_Phi[i, :] for i in 1:n_inter} if environment.analysis and n_inter > 0 "Time constants for translational inter-phase exchange"; output Q.TimeAbsolute tau_QE_intra[n_intra]( each stateSelect=StateSelect.never, each start=U.s) = c_p*nu*k_intra_Q if environment.analysis and n_intra > 0 "Time constants for thermal intra-phase exchange"; output Q.TimeAbsolute tau_QE_inter[n_inter]( each stateSelect=StateSelect.never, each start=U.s) = c_p*nu*k_inter_Q if environment.analysis and n_inter > 0 "Time constants for thermal inter-phase exchange"; // Note: The structure of the problem should not change if these auxiliary // variables are included (hence, StateSelect.never). // // Translational momentum balance output Q.Force f_DE[n_trans](each stateSelect=StateSelect.never) = sum(intra[ i].mPhidot for i in 1:n_intra) + sum(inter[i].mPhidot for i in 1:n_inter) if environment.analysis "Friction from other configurations (diffusive exchange)"; // // Energy balance output Q.Power Edot_DE(stateSelect=StateSelect.never) = sum(intra[i].phi* intra[i].mPhidot for i in 1:n_intra) + sum(inter[i].phi*inter[i].mPhidot for i in 1:n_inter) + sum(intra.Qdot) + sum(inter.Qdot) if environment.analysis "Rate of diffusion of energy from other configurations"; Connectors.Intra intra[n_intra](each final n_trans=n_trans, each T(final start=T_IC, final fixed=false)) "Connectors to exchange translational momentum and energy within the phase"; Connectors.Inter inter[n_inter](each final n_trans=n_trans, each T(final start=T_IC, final fixed=false)) "Connectors to exchange translational momentum and energy with all other species"; Connectors.Dalton dalton(V( min=0, final start=V_IC, final fixed=false), p(final start=p_IC, final fixed=false)) "Connector for additivity of pressure"; // Geometric parameters protected outer Q.Volume V "Volume of the phase (not of the subregion)"; outer parameter Q.Length L[Axis] "Lengths of the subregion"; outer parameter Integer cartTrans[:] "Cartesian-axis indices of the transport axes"; // Note: The size of cartTrans is n_trans, but it can't be specified here // due to an error in Dymola 2014. outer parameter Q.NumberAbsolute k_inter_Phi[:, :] "Independence factors for translational exchange with other phases"; outer parameter Q.NumberAbsolute k_inter_Q[:] "Independence factors for thermal exchange among with other phases"; // Note: The sizes can't be specified due to an error in Dymola 2014. outer Conditions.Environment environment "Environmental conditions"; initial equation // Check the initial conditions. assert(V >= 0, "The volume of " + getInstanceName() + " is negative. Check that the volumes of the other phases are set properly."); equation // Aliases (only to clarify and simplify other equations) h = g + T*s; p = dalton.p; v*N = dalton.V; M = Data.m*N; // Thermodynamic correlations h = Data.h(T, p); s = Data.s(T, p); // Exchange // -------- // Within the phase for i in 1:n_intra loop k_intra_Phi[i, :]*mu .* intra[i].mPhidot = N*(intra[i].phi - phi) "Translational"; k_intra_Q[i]*nu*intra[i].Qdot = N*(intra[i].T - T) "Thermal"; end for; // // With other phases for i in 1:n_inter loop k_inter_Phi[i, :]*mu .* inter[i].mPhidot = N*(inter[i].phi - phi) "Translational"; k_inter_Q[i]*nu*inter[i].Qdot = N*(inter[i].T - T) "Thermal"; end for; end Species;